What if Segal/Cover Scores Were Perfect?

What would judicial reality look like if Segal/Cover scores perfectly predicted the liberal tendencies of the justices? Just so there is no confusion, note that one might approach a question like this from “two ends.” One could simply change the Segal/Cover scores so that they perfectly matched the career-liberal ratings of justices in civil liberties cases – creating, in essence, a logit model that regresses career percentages against justice votes – or one could change liberal ratings to reflect what Segal/Cover scores purport to say about them (in theory). It is the latter transformation that I will undertake in this entry. (The former will be undertaken later).

To do this one must ask a central question: if justices voted exactly according to their newspaper reputation for political direction, what would that look like? One answer might be that a perfect match occurs when the propensity for bias found in the reputation has a one-to-one correspondence with the propensity for bias found in the actual votes. Hence, perfect prediction might simply be the scaled Segal/Cover scores.[1]  A justice having a Segal/Cover score of 0, therefore, would be expected to have a liberal output of 50% if newspaper reputation perfectly measured and predicted an aggregate directional tendency.[2]  (For those who object that perfect prediction would not exist using one-to-one proportionality, hold off for just a second).

So what would reality look like if Segal-Cover scores were perfectly accurate, using one-to-one proportionality? To answer this question, I have conducted a logistic regression of simulated data for all civil liberties votes cast for all justices from 1946-2004. (The data is uploaded on this website and can be accessed below). It was fairly easy to create the simulated votes. I simply changed the vote distribution of each justice in my real data set so that the proportion of liberal votes matched perfectly the scaled Segal/Cover score. For example, Justice White has 2,307 votes in the data set and his Segal/Cover score is 0 (scaled to .5); therefore, his vote distribution was changed to 1154 liberal, 1154 conservative.

The results of the regression are quite interesting and can be found in the following table. As one can plainly see, this regression is immaculate. They should put it in an attitudinal museum. The likelihood-ratio R-squared is .38, which is an excellent number for a bivariate ideology model.[3]  According to PRE (tau-p), knowing the newspaper reputation of a justice increases the ability to classify votes by 59%. Phi-p indicates that the overall voting variance accounted for by the model is about 59% as well, which is the level of explanation that Segal and Spaeth originally thought they had created with ecological regression. The regression coefficient also supports a rosy scenario. The KDV shows that when Segal-Cover Scores change from -1 (most conservative) to +1 (most liberal), the discreet change in the probability of obtaining liberal votes increases by .9999, a near perfect match.[4]  The only way this model can become better as far as goodness of fit is concerned is to eliminate the perfectly non-directional justices having “neutral” political reputation (White, Whittaker and Clark).

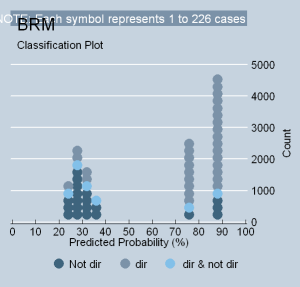
To see why this model performs so well, examine the classplot below. As one can plainly see, the model is superb simply because it is anchored with extreme values for the predicted Y, with relatively little obstruction coming from the middle-range values. In short, there are two distinct voting clans that dominate the model. Hence, if Segal-Cover scores were perfectly true (using a one-to-one correspondence), the reality that would exist would probably best be described with the following statement: “Rehnquist votes the way he does because he is extremely conservative; Marshall voted the way he did because he was extremely liberal.” (Segal and Spaeth, 2002, 86; 1993, 65).

There is still one disturbing objection, however: isn’t it ridiculous to have a hypothetical model where Justice Scalia never votes liberal? My answer at this point is to hedge a bit: this was only a hypothetical exercise. Because some may believe that a better model of perfect prediction should be something less than a one-to-one correspondence, I will adjust the numbers tonight and post a second analysis. I’ve got an idea of what to do.

Data: http://ludwig.squarespace.com/file-download/segal-cover.perfectpred.dta

[1] Segal-Cover scores “count” from -1 to +1, which is 200 increments. The liberal ratings “count” from 0 to 100, which is 100 increments. To scale the Segal-Cover scores, simply transform them by the formula 1 – (.5 - (score/2)). 

[2] So long, of course, as the propensity for political direction remained constant in the values of a justice throughout his or her term on the bench, and so long as the dichotomous vote-coding construct used by political scientists accurately captured its subject (a controversial proposition that I have not yet addressed).

[3]. It is extremely rare for a bivariate ideological model to achieve a value of R²L above .4. In the hundreds of bivariate regressions I have performed, I have never seen a value that high. Therefore, I would suggest that at the outset researchers involved in bivariate ideology models adopt a simple rule of thumb: R²L values between .2 and .4 are “quite good results” and values below .1 are a baseline for results that are “not so good.”

[4] The relationship between the discreet change in the probability of Y for each 10% increase in X does not appear to be linear, however. For some 10% changes in X, the discreet change in the probability of Y is more extreme than for other 10% increments. The KDV reported in the table is the sum of all of these changes.

Ideology Models Only Account for 12.5% of the Votes!

I need to make a clarification about something. On several occasions – both in here, on Howard’s list and on ELS – I stated that newspaper reputation accounts for only 24% of the votes that justices cast in civil liberties cases over the last (almost) 60 years. That figure may be somewhat misleading. I grabbed it from phi-p, which is a correlation statistic used in contingency-table analysis. But whether or not it is misleading, one of the things that is undeniable is that in the ecological regression of civil liberties votes endorsed by numerous political science scholars, only 12.5% of the total votes cast in civil liberties are responsible for the 41% of the variance in the liberal index that newspaper reputation “explains.” Only 12.5%!! Let’s take a closer look.

As I have demonstrated previously, the R-squared in an ecological regression involving Segal/Cover scores and career liberal ratings in civil liberties cases from 1946-2004 is 0.41. Keep in mind that this figure is not the explained variance of the votes; it is the explained variance in the numbers comprising the liberal index. To equate the one with the other is an ecological fallacy. To see just how damaging this fallacy is, I have provided a table which looks closely at what this R-squared statistic is reporting. The table can be accessed here.

The table is useful for several reasons. First, it breaks down the explained and unexplained variance that occurs in the numbers comprising the liberal ratings. It also, however, breaks down the number of justice votes implicated by those percentage points. As one can plainly see, the number of votes that accompany the explained portion of the regression is only 12.5% of the total number of votes that comprise the entire regression (31,049). That means the regression is only able to rely upon 12.5% of the votes to explain 41% of the variance in the ratings.

Another thing that is interesting is how each justice is affecting (or driving) the R-squared. This can be located in the column to the far right, called ERL (Explained Ratings Load). This column is simply referring to the contribution that each justice is making to the R-squared statistic (the explained variance). The justices who are actually driving the statistic the most are the ones who carry the highest proportion of influence (“load”). Scalia is a good example; he accounts for over 6% of the R-squared by himself. Justice Rehnquist is right behind him.

But now, however, examine the column titled EVL (Explained Voting Load). This column shows the proportion of votes that are hiding behind each of these “rating loads.” This is simply the proportion of the 12.5% of the total votes to which each justice contributes. Here we find something else of interest. First, there are, as one might expect, some justices who “artificially” contribute to the R-squared by having “payoffs” in their percentage points that are not matched by their votes. Good examples of this are justices Goldberg, Fortas, Rutledge, Jackson and Thomas (to some extent). To see this better, examine the following graph (the red lines of those justices – the percents – are disproportionate to the grey lines, the votes). Also, of the 12.5% of the votes that are needed to drive the 41% of the ratings, the bulk of the work comes disproportionately from four key justices: Rehnquist, Blackmun, Brennan and Douglas.

I’ll have more to say about this in a couple of days. I’ve got to run now.

What Causes These Ideology Models to Fail?

[Version 2]*

In my last entry, I showed that newspaper reputation for political direction did not constitute as significant or substantial of an explanation of voting behavior as many political scientists had suggested over the last sixteen (16) years. Although its performance may be perfectly acceptable to some, clearly, others in the discipline seem to wish it would be strong enough to explain the bulk of what the Court does in civil liberties cases (which it does not). In this entry I take up the issue of why ideology models do not perform better.

The answer is straight forward: there are simply too many justices who do not affiliate well with the binary outcome being analyzed by the model. If a logit model was a drain, centrists justices are the clog. And that means that “newspaper ideology models” are really nothing other than a partially-clogged piece of plumbing. To demonstrate this, examine the stepwise analysis (Table 5 in my SSRN paper). It begins with the logit results of Segal and Spaeth’s base ideology model, updated to 2004. It then subtracts the justice with a liberal rating closest to pure non-direction (.5) and re-estimates the regression. The subtraction continues one justice at a time until only those justices with ratings above 66.1 (Ginsburg) and below 33.9 remain. The subtraction increment is 16.1 points above or below 50%. As each median justice is subtracted, the values of the regression increase remarkably. At the very end of the regression, Justice Douglas is added. By this time, the only justices remaining in the analysis are the following ten: Brennan, Burger, Fortas, Goldberg, Marshall, Rehnquist, Scalia, Thomas, Warren and Douglas.

The table is simply amazing. The model has been transformed from “clogged plumbing” to Niagara Falls. It now has a KDV of 78 points and increases the ability classify the direction of votes by 57%. The total voting variance explained by the model is also 57% (phi-p). Or, stated another way, “Rehnquist votes the way he does because he is conservative; Marshall voted the way he did because he is liberal.” To really see the effect of “clan voting,” examine the classification plot below. It shows quite clearly why the model performs so well: there are no justices clustered around the 50% mark, and the model has two solid anchors on each side:

What does this show? It demonstrates is that one cannot create a bivariate ideology model that has the level of explanation that Segal and Spaeth originally believed they had created – a model that explains at least 60% of the Court’s choices – without first removing every justice from the truncated model having a liberal rating within 34% and 66.2% (and adding Douglas).[i] What this also says is that scholars who are championing the idea of an ideologically-driven Court are simply allowing the votes of those justices with the most obstinate judicial personalities to stereotype the majority of the institutional-membership’s voting behavior.

To see this, consider the model in Table 6 of my SSRN paper. It analyzes civil liberties voting from 1946-2004, but excludes 8 of the most directional justices having liberal ratings below 23% and over 77% (Rehnquist, Goldberg, Fortas, Douglas, Marshall, Brennan, Murphy and Warren). One of the reasons why excluding outliers is relevant, of course, is that the current Court no longer contains membership with career propensities beyond the values being excluded. Hence, one could argue that this analysis is a better estimation of the degree to which justice ideology governs votes on the current Court, [ii] at least to the extent researchers claim to have observed such phenomena in the Supreme Court data base.

The result of the subtraction is simply remarkable. The index variance explained by the regression drops to 17%. Total voting variance drops to 9% (phi-p), and PRE is only 11% (tau-p). The coefficient in the logit regression indicates that liberal ratings only increase by 8 discreet points as Segal/Cover scores change by 100% (KDV). The classplot in Table 3, Figure 6, speaks for itself. But what is perhaps more interesting is what happens if the subtraction range is increased by one percentage point in each direction (24% to 76%). It results in the exclusion of only two additional justices (Thomas and Rutledge) and produces a statistically-insignificant ecological model. [iii] It is indeed remarkable that an ecological model is completely unable to explain the liberal ratings of nearly two-thirds (22) of the Court’s membership since 1946, and that, whatever level of explanation it otherwise achieves is simply driven by a small minority of the Court’s most obstinate personalities.

---

[i] Some may be tempted to object that this manuscript sets up a test of the attitudinal model that requires justices to vote perfectly liberal or conservative before “attitudinalism” can prevail. This is not accurate. The manuscript merely requires that the career choices of the largely non-directional justices be similar to the directional before the bivariate model can be regarded as systemically dominant as proponents of ecological regression claimed. Indeed, what this manuscript demonstrates is only that what researchers empirically operationalized as “attitudinalism” simply plays a smaller role than previously thought. Finally, it should be remembered that there are three pathways to higher numbers in these models: (a) extreme justices voting with less dependency (see Figure 2 in Table 3); (b) middle justices voting like affiliated ones; or (c) some combination of the two.

[ii] Although the career propensities of Justices Alito and Roberts are not yet known, it is perhaps worth mentioning that both justices are predicted to be in the “moderately conservative” range. Alito’s newspaper reputation for political values was -0.8. His career liberalism is estimated to be 0.355 using a logit model and 0.343 using an ecological model. Justice Roberts’ newspaper reputation, by contrast, was -0.76, making his estimated liberalism 0.364 (logit) and .351 (ecological). However, it must be remembered that these forecasts are not remarkably accurate. The absolute value of the average mistake is 13 points for ecological regression and 13.1 for logit regression. Therefore, one cannot say that Alito or Roberts will not be especially directional. This caveat must be kept in mind when considering whether a regression that excludes outliers is a more accurate model of today’s Court.

[iii] There are other voting circumstances where Segal/Cover scores produce statistically insignificant results in civil liberties cases. Newspaper reputation is a statistically insignificant predictor (p values greater than .1) for every civil liberties vote cast by justices in the years of 1950, 1954, 1964, and 1992 (95% confidence interval, two tailed test). The p-values are also greater than .01 for the years 1949, 1951, 1952, 1953, 1965, 1968, 1991 and 1993 (Wilson 2006).

* substantial edit

The Truth About "Newspaper Ideology" and Civil Liberties Voting, 1946-2004

[Version 2.0]*

I have just spent a week laying out an indictment against the bivariate ideology models that political scientists constructed over the last sixteen years. The indictment is predicated on a basic point: the aggregation of voting data and resulting misinterpretation of the R-squared statistic caused the creation of disciplinary misinformation – empirical falsehoods, plain and simple, that were passed along to political science graduate students and the rest of the academic community. Now is the time to correct these falsehoods by constructing a bivariate ideology model that avoids ecological inference and correctly estimates the relationship between model variables.

First, however, keep in mind a couple of things. I have yet to say anything about the propriety of the measures in these models. Some have said that the stuffing of justice opinions into one of two binary outcomes – liberal or conservative – or the fitting of justices’ preferences in unidimentional space is too simplistic to merit serious consideration. I will visit these issues at a later date. But for now, all that I want to do is find a more simplistic truth: how well do these measures actually perform when researchers model them properly and understand the results?

Below are the results of a logistic regression of civil liberties voting from 1946 to 2004. The regression contains 31,049 votes cast by 32 justices over 58 years of service on the high Court. The data is publicly available from the Ulmer project. [1] Let’s discuss goodness-of-fit first. The first indication that the fit of the model is poor is the rather low value (0.067) of the likelihood ratio R-squared. [2] The second indication that the fit is not that great comes from the PRE measures. Of the three that are listed, tau-p is the best for judicial modeling. [3] Tau-p indicates that the model only increases the ability classify liberal votes by 24%. Also, Phi-p, which is calculated using the logic of Pearson’s r, suggests that the overal variance between Segal-Cover scores and justice votes is about 24% The table can be accessed here.

Although analyzing the goodness of fit of a logit regression may not be as easy as an OLS regression, one of the nice things is that both now have the ability to generate a "picture." Take a look at the STATA “classplot” below. It shows why the fit of the model is not very satisfying. The reason is twofold: (1) too many justices are simply “non-directional” (median justices who do not affiliate well with dichotomous choices pull down the model’s fit); and (2) there is not enough “gusto” coming from each end of the value spectrum (no one is predicted to vote in the very extreme ranges of 0 to 29, or 80-100). In short, there is too much traffic around the value of 50% and not enough around 20 or 80. That’s why the numbers are poor.

Now let’s look at the coefficient. I like to focus on what I call the "key" discreet change or value (KDV). This statistic shows the total discreet amount that predicted ratings change as Segal-Cover scores change from their minimum to maximum values. Hence, going from absolute conservatism (-1) to absolute liberalism (+1) -- a 100% change – causes predicted liberal ratings to increase by 41 points, less than half the proportion of the change in values.[i]  Stated another way, newspaper reputation is less than half of the story, even using coefficient logic.  And although these results may be perfectly acceptable to some – they certainly seem to fit a Pritchett framework -- it is quite clear as an empirical matter that they do not: (a) explain the bulk of choices justices cast in civil liberties cases; or (b) establish the mythology of judging by showing the supremacy of political values.   Therefore, the ultimate point is that the reputation a justices obtains for political direction at the time of his or her confirmation does not explain nearly as much of the voting universe as the political scientists who originally constructed or endorsed these models proclaimed. This conclusion is not a matter of opinion; it is true as a simple fact of how data is interpreted and analyzed in a statistical model.

Because some scholars (Segal at al., 1995) believe that ideology models perform better when eliminating justices who predate the Warren Court, it is necessary to consider models that exclude Truman and Roosevelt appointees (the “truncated model”).  The findings are found in Table 4 of my SSRN paper.  It indicates that the truncated model is really no different from the model that contains all of the justices. The fit is poor (0.070 R²_L); the increase in the ability to classify liberal votes is moderate (24%, tau-p); and the total voting variance is about 24% (phi-p). The predicted magnitude of the variable relationship is also roughly equal to a model containing all of the justices (KDV = .418). The classplot below is virtually indistinguishable from the preceding one.  Although it is true that a higher proportion of index variance is present in the shorter list of ratings, only 14.6% of the model votes drive this effect (see Table 8 in my SSRN paper) [ii] and only five justices are responsible for half of it. [iii]  Therefore, the substantive conclusions drawn from a model of a truncated set of justices is really no different from the full model.

REFERENCES:

Menard, Scott. 2002. Applied Logistic Regression Analysis. Thousand Oaks: Sage Publications. 20-27.

Kleckla, W.R. (1980). Discriminant Analysis. Thousand Oaks: Sage Publications. 7-19.

DeMaris, Alfred. 1992. Logit Modeling, Practical Applications. Thousand Oaks: Sage Publications. 53-54.

---

[1] My particular data set is an integration of the Vinson Court data and the original Supreme Court data (updated through 2004). I transformed the data into a single “justice-centered” set with the help of Paul Collins.

[2] R2L is sometimes called “the McFadden R2.” According to Menard (2002), the statistic has the desirable properties of running from 0 (no fit) to 1 (perfect fit), is not affected by the proportion of cases in the sample having the attribute 0 or 1 (called the “base rate), and is not affected by the sample size of the data. However, it is important to remember that R2L is only an analogue to the OLS R2; the two statistics cannot be directly compared. Clearly, R2L underestimates goodness-of-fit when compared to OLS estimations of continuous-level data (DeMaris 1992, 53-54), and cannot be considered itself an explanation of overall voting variance (Menard, 20-24). It is extremely rare, moreover, for a bivariate ideology model to achieve a value of R2L above .4. In the hundreds of bivariate regressions I have performed, I have never seen a value that high. Therefore, I would suggest that researchers involved in bivariate ideology models adopt a simple rule of thumb: R2L values between .2 and .4 are “quite good results” and values below .1 are a baseline for results that are “not so good.”

[3] Based upon Menard’s (2002, 32-34, 36) reasoning, lambda appears inappropriate for a bivariate ideology model because it assumes that errors without the model take the form of an all-or-nothing guess (Menard, 29). In essence, lambda would only be helpful as a PRE measure if modelers could theoretically make the assumption that in the absence of any knowledge of their X variable, every justice in their sample of cases would vote unanimously in every case, the entire sample being all liberal or all conservative. Obviously, this does not appear to be a reasonable assumption.The measure that is best, therefore, for judicial politics scholars is Klecka’s (1980) index originally proposed for use in discriminant analysis models, generally referred to as “tau.” Following Menard’s terminology (2002, 32), I denote the term “tau” with a “p” – tau-p – to indicate its application to a 2 x 2 prediction table generated by a logit model. Tau-p is simply the best PRE statistic for judicial modelers because it assumes that the goal of the logit model is simply to classify as many liberal/conservative votes that are actually found in the base rate of the sample. Therefore, tau-p does not assume an all-or-nothing guessing scenario. It assumes that the number of liberal and conservative votes to be “guessed” in the absence of knowledge about the values of X is simply the proportion of liberal and conservative votes actually present in the sample. In this sense, Menard says that tau-p is less concerned with prediction logic and more concerned with classification logic. (29,33). Of course, like all PRE statistics, tau-p becomes problematic if data becomes excessively skewed.

[i] But how accurate are these predictions? Regressing the predicted liberal score of each justice against the actual ratings produces an R-squared of .4081, indicating that the logit predictions account for roughly 41% of the index variance. (Table 4 lists this statistic as “ppeR²,” which refers to “predicted probability R²”). Note that this is the same amount of index variance reduced in the ecological model. But note also how misleading this can be: As Table 8 shows, the ecological model only uses 12.5% of the Court’s votes to explain 41% of the index variance. And as both the logit model and Table 7 shows, there does not appear to be much overall political direction in the index in the first place.

[ii] Table 8 analyzes the explained and unexplained variance in the ecological model’s R-squared. As one can plainly see, the number of votes that accompany the explained portion of the regression is only 12.5% for the full model and 14.6% for the truncated model.

[iii] Note on Table 8 that only five extreme justices – Brennan, Fortas, Marshall, Scalia and Rehnquist – contribute 56% of the truncated model’s R². When compared to the full model, however, those same justices cannot carry such “loads” – they account for only 37% of the explained variance.

* substantial editing.

Ecological and Logit Predictions of Liberal Ratings

[version 2.0]*

After having my head under the hood of Segal-and-Spaeth’s bivariate ideology model over the last week, I discovered something interesting: ecological regression does not effect how efficiently Segal/Cover scores predict aggregate liberalism on the Court. I had suspected the opposite. Although the two sets of predictors are quite similar and their overall difference is small, there does appear to be one interesting pattern: logit regression predicts liberal justices slightly better while ecological regression predicts conservative justices slightly better. Overall, ecological regression predicted 18 justices better; logit regression predicted 14 better. The best way to demonstrate these findings is by examining the following table and a graph. (Click bold words to access. Look at the output yourself. The graph really shows the story the best. A picture is worth a thousand words).

To explain the findings better, consider the Court’s two newest voters. Just how conservative will Alito and Roberts be? I’ve uploaded another table that analyzes the data.[1]  Alito’s newspaper reputation for political values was -0.8 (see Jeff Segal’s website). That means Alito’s career liberalism is estimated to be 0.355 using a logit model and 0.343 using an ecological model. Justice Roberts’ newspaper reputation, by contrast, was -0.76, making his estimated liberalism 0.364 (logit) and .351 (ecological). In short, both of the new justices are predicted to have a liberal tendency roughly equal to the aggregate tendencies of O’Connor, Kennedy and Powel (to say nothing of the policy differences that will comprise this tendency).

Now the big question: how accurate are these forecasts? The answer is: not incredibly. The average mistake that these forecasts generate is 13 points for ecological regression and 13.1 for logit regression. That means that, on average, Alito could be the next Rehnquist or the next (almost) Stewart. But at least we have a reasonable basis (before he takes the bench) for knowing that he is not the next Stevens or Brennan. Interestingly, if you regress the predictions generated by newspaper reputation against the reality that eventually emerges (the true aggregate liberalism), the R-squared is .4117 for ecological predictions and .4081 for logistic ones. Hence, ecological regression does not affect how well Segal/Cover scores can forecast predictions of an aggregated tendency. But in either case the quality of the forecast that emerges is “partly cloudy.”

---

[1] The table shows not only the difference between ecological and logit estimations, but also the difference between estimations based upon modeling decisions that exclude Truman and Roosevelt appointees versus those that do not. There is some controversy about whether these justices should be excluded. My view is that they should not be. I hope to author an entry about that point later.

* excised unnecessary final paragraph and changed the title.